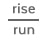Interpret the Slope of a Graph
Middle and Upper Level
ISEE Question: The graph of a line is shown.
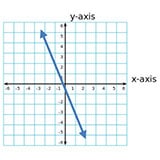
What is the slope of the line?
A) -3
B) -2
C) ½
D) 3
The slope is the steepness of a line. To approximate the slope, observe how the line moves from left to right.
Solution:
STEP 1: Identify whether the slope is positive, negative, or zero.
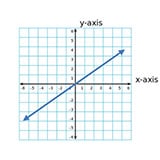
If the line goes up,
its slope is positive:
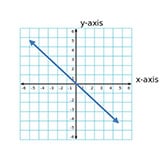
If the line goes down,
its slope is negative:
If the line is exactly horizontal,
its slope is zero:
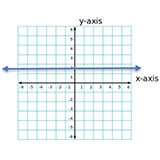
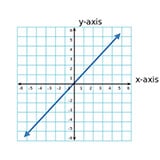
STEP 2: Identify whether the slope is greater than, less than, or equal to 1 or -1.
A perfectly diagonal line (assuming that both axes have the same scale) that moves up as you move to the right has a slope of 1. If it moves down, it has a slope of -1.
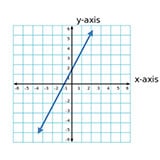
A line that is steeper than a perfectly diagonal line has a slope that is more than 1 or less than negative 1.
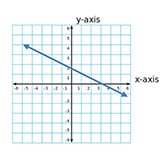
A line that is less steep than a perfectly diagonal line has a slope that is a fraction less than 1 or more than -1, such as ½ or -¼.
STEP 3: Once you’ve eliminated the incorrect answers, you might be down to the correct answer already. If not, locate two points that fall perfectly along the axes. For example, in the original question, the points (0, 0) and (1, -3) fall exactly along the grid lines.
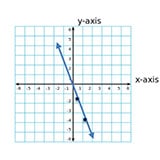
STEP 4: Use the formula for finding the slope from two points (link) to determine the